Energy Equation Proposes Patterns of Weight Gain and Loss

Controlling body weight is a simple matter of balancing how much you eat against how much you burn, right? For some, maybe, but HMS researchers have devised a mathematical model of energy balance and body weight that suggests a more complicated equation.

The model predicts that mice susceptible to developing resistance to the metabolic regulator leptin have multiple stable body weights. Simulated mice based on the model grow obese after overeating, eventually hitting a high stable weight. But losing this weight and returning to a lower stable weight can be extraordinarily difficult. Though the model blends two competing theories of body weight, it departs from their predictions that body weight gravitates to one stable weight or weight range. If the model proves correct, it may point to new interventions to help ease weight loss even in the most intractable cases.

It may seem odd that this model of metabolism comes from the lab of a tumor biologist, Rakesh Jain, the A. Werk Cook professor of radiation oncology (tumor biology) at Massachusetts General Hospital. But to Jain, a chemical engineer trained to think in terms of systems and controls, it is perfectly natural. In fact, his career in tumor biology began with a mathematical model of pressure differentials in tumors. Jain got into obesity research when he learned that leptin, in addition to regulating body weight, may also regulate blood vessel formation.

Joshua Tam, a doctoral student in the Harvard–MIT Division of Health Sciences and Technology and also a chemical engineer, picked up on Jain’s interest. He saw parallels between engineering control systems and the body’s system to regulate weight, so he wanted to see if the engineering tools fit. Tam is first author of the January Cell Metabolism paper that describes the resulting model.

Drawing on decades of experiments in mice, Tam defined a set of equations that simulates their collective results. He began by creating two models, each aligned with one of the two prevailing theories of body weight regulation. One, the set point model, works much like the cruise control system in a car. The leptin system in the body aims to maintain a constant body weight by adjusting the desire for food and the burn rate. The other, the settling point model, is a more open-ended system. Tam likened it to a water faucet; adjusting the hot and cold taps results in a water temperature that settles in a given range.

Though Tam built both models on experimental evidence, neither fit perfectly with all the evidence. Simulated mice representing the set point model never remained obese; their weights always returned to the set point. This contradicted evidence of diet-induced obesity in live mice. The settling point model contradicted evidence in the case of starvation.

So Tam decided to combine the two models. The unified model uses the set point theory to simulate the case of starvation, but when leptin levels in the brain cross a certain threshold, the settling point dynamics take over. This kind of combination, said Jain, is very common in thermodynamics. “You develop it based on one phase, then another phase, then you mix it together.”

It is not, however, common in biology. Co-author Dai Fukumura, HMS associate professor of radiation oncology at MGH, played a large role in this work by acting as a translator. He helped Tam and Jain ground their model in biology and also helped them change their engineering-centric (and, to them, “common sense”) explanations into more accessible terms.

Another element Tam added to the models was a way to simulate leptin resistance. Leptin is a hormone produced by fat tissue. It crosses the blood–brain barrier and signals the body to stop eating. In its absence, the body craves food. A decreased sensitivity to leptin results in unnecessarily high food intake, so it is thought to be a cause of diet-induced obesity. It is also thought to be a consequence of obesity because, as fat stores increase, leptin concentrations also increase, eventually triggering the development of resistance.

Little research has been done, however, to quantify resistance or the dynamics of this feedback loop. “There really isn’t a lot of data to draw on,” said Tam. This dilemma points out one of the central values of mathematical models to biology: “They force you to list what you know and what you don’t know.”

“What mathematics does, essentially, is write the hypothesis in equations,” said Jain. “You can’t just hand-wave without quantifying how much waving you are doing. You have to make tough choices whenever you write an equation.”

Defining leptin resistance mathematically was tough. Tam settled on a model that increases leptin resistance linearly once leptin concentration in the blood crosses a threshold. The dynamic is reversible, so as leptin concentration drops, resistance wanes. “The assumptions I made might turn out wrong when you do the experiments,” said Tam, but those findings, in turn, will lead to the next best model.

By bringing leptin resistance into his unified equations, Tam found that simulated mice had multiple steady states for their body weight. “It’s a beautiful discovery,” said Jain. “In a way, it explains why some thin people remain thin no matter how much they eat, while people who are overweight have difficulties in lowering their body weight.”

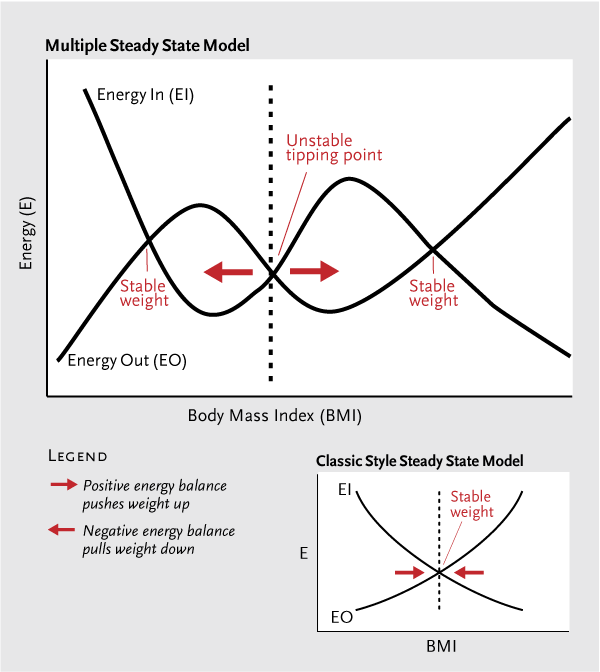
Different individuals, based on their genetics and behavior, may have one, two, or more stable weights. Simulated mice that are not susceptible to leptin resistance, for example, have one stable weight. Add leptin resistance and, in the simplest case, two stable weights emerge (see diagram). A third weight—which is unstable—acts as a tipping point between the low and high stable weights.

Once this tipping point is crossed on the high side, the body gravitates toward the high weight even if the lower weight is closer. To reach the lower weight, the body must first fight its way through the forces impelling it toward the high weight until it passes the tipping point. “If you can change these curves”—perhaps, someday, with a drug that increases leptin sensitivity—“you can make it easier for people to get from one state to the other,” said Tam.

“That’s the exciting point. It brings some hope,” said Jain. “But for human beings, these equations are not yet known.” This new hypothesis, written in mathematical terms, calls out for further experimentation, such as investigations into leptin resistance and explorations into how other hormones besides leptin regulate energy balance. “It’s a well-defined prediction,” said Jain. “But it has to be validated.”

Students may contact Rakesh Jain at jain@steele.mgh.harvard.edu for more information.

Conflict Disclosure: The authors report no conflicts of interest.

Funding Sources: The National Institutes of Health